We continue our study of Jacobi fields. We get a closed form expression for Jacobi fields vanishing at a point, and make a connection with curvature.

Jacobi fields vanishing at a point

Let $J: [0,\pi] \to TM$ such that $J(0) = 0$. Then the geodesic variation $\Gamma(s,t) = \exp_{\sigma(s)}(tW(s))$ has a certain form which gives a nice formula for $J$.

Here we shall make use of the identification \(T_v T_p M \simeq T_p M\) for $p\in M$ and $v\in T_pM$.

Diagram showing geodesic variation

For the differential of a function $f:M\to N$ between manifolds we shall use the notation

\[( df )_{p} : T_pM \to T_{f(p)}N\]

at each point $p\in M.$

Lemma 2 (explicit form of zero-start Jacobi fields)

Let $\gamma: [0,1] \to M$ be a geodesic, $p = \gamma(0)$, $v = \gamma’(0)$. Let $J: [0,\pi] \to TM$ be a Jacobi field such that $J(0) = 0$, $J’(0) = \frac{D}{dt}J|_{t=0} = w.$

Then $J(t) = (d\exp_p)_{tv}(tw).$

Proof

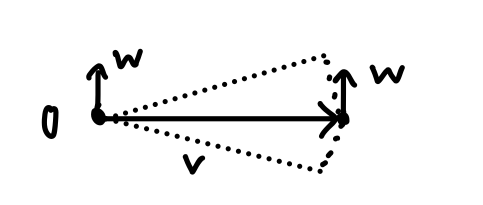
We have $\gamma(t) = \exp_p(tv)$. Consider the variation $(s,t)\to \exp_p(t(v + sw))$.

Since each $\gamma_s := \exp_p(\cdot(v+sw))$ geodesic, it’s a geodesic variation.

Diagram showing exponential map variation

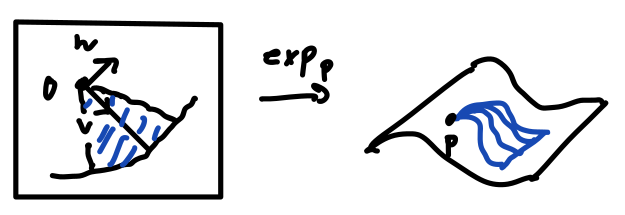
Recall that the exponential map at a point $p$ is a function $\exp_p: T_pM\to M$. Thus by the chain rule,

\[\begin{align*} J &= \partial_s \exp_p(t(v+sw))|_{s=0}\\ &= (d\exp_p)_{t(v+sw)} \partial_s t(v+sw)|_{s=0}\\ &= (d\exp_p)_{tv}(sw), \end{align*}\]

is a Jacobi field.

$\square$

By our identification $T_vT_pM\simeq T_pM$, the differential of the exponential map maps as follows.

\[(d\exp_p)_v: T_pM \to T_{\exp_p(v)}M.\]

Gauss Lemma

Let $p \in M$, $v \in T_p M$ such that $\exp_p tv =: \gamma(t)$ is defined for $t \in [0,1]$. Then,

\[\langle (d\exp_p)_v(v), (d\exp_p)_v(w) \rangle_{\gamma(1)} = \langle v,w \rangle_p, \quad w \in T_v T_p M \simeq T_p M\]

Proof

We know that $J(t) = (d\exp_p)_{tv}(tw): [0,1] \to TM$

is the Jacobi field along $\exp_p tv$ such that $J(0) = 0$, $J’(0) = w.$

The tangential Jacobi field such that $J(0) = 0$, $J’(0)=v$ is simply $t\gamma’(t)$. This is since the Jacobi equation reduces to $J’‘=0$ since $R(J,\gamma’)\gamma’=0$ by the symmetries of the Riemann curvature.

Let $T_pM\ni w = \lambda v + w_\perp$ such that $\langle w_\perp, v \rangle = 0.$ First, notice

\[\langle v,w \rangle = \lambda |v|^2 = \lambda.\]

By linearity of the differential,

\[\begin{align*} J(t) &= (d\exp_p)_{tv}(t\lambda v + tw_\perp)\\ &= \lambda (d\exp_p)_{tv}(tv) + (d\exp_p)_{tv}(tw_\perp)\\ &= \lambda t \gamma'(t) + J_\perp(t), \end{align*}\]

where \(J_\perp(t):=(d\exp_p)_{tv}(tw_\perp)\) is the perpetually normal Jacobi field such that $\langle J_\perp(t), \gamma’(t) \rangle = 0.$ Remember Proposition 1 from the previous note.

So

\[\begin{align*} \langle (d\exp_p)_v(v), (d\exp_p)_v(w) \rangle &= \langle \gamma'(1), J(1) \rangle \\ &= \lambda |\gamma'(1)|^2 + 0 \\ &= \lambda \end{align*}\]

since $\gamma$ is parametrised by arclength (i.e. unit speed).

$\square$

Take $r>0$ small enough so that $B := \exp_p(B_r)$ is the geodesic ball ($B$ and the ball of radius $r$ in the tangent space are diffeomorphic.) We denote by $S_r$ the sphere $\partial B_r.$ A vector $v\in S_r$, is such that $v\in T_pM$ with length $|v|=r$.

Since the exponential map is a diffeomorphism around $B_r$, we have that \(S := \partial B = \{q\in M : d(p,q)=r\} = \exp_p(S_r).\) Indeed, $\exp_p(v)$ is the point which you reach by traveling along the geodesic starting at $p$ in the direction $v$ for a length $|v|$. Geodesics $\exp_p(tv)$ are thus called radial.

Take a vector $v\in S_r$ such that $|v|=r$. Pick a tangent vector to the sphere $w \in T_v S_r \simeq T_p M$ such that $\langle w,v \rangle = 0$.

Let $\gamma(t) = \exp_p(tv)$ be the radial geodesic of $v$. Let $J_w(1)$ denote the Jacobi field $(d\exp_p)_{tv}(tw): [0,1] \to TM.$ Then by the Gauss Lemma, $\langle \gamma’(1), J_w(1) \rangle = 0$.

We have that $\gamma’(1)$ is tangent to the radial geodesic at $\exp_p(v)$. Therefore, $J_w(1)$ is tangent to the hypersurface orthogonal to that radial direction — i.e., it’s tangent to the geodesic sphere $S$ at $\exp_p(v).$

In other words, the geodesic sphere is a hypersurface orthogonal to the radial geodesics starting from $p$.